Перевод статьи Sailing through Rough Winds of Macroeconomic Risks (by Samir Shah, Tillinghast–Towers Perrin, June 2000)
Если ссылка выше не доступна, то оригинал также можно прочитать в файле Sailing.doc (формат - MS Word, 169.5 кб)

Кто бы мог предположить 3 года назад, что Азиатские валюты потеряют 40-80 процентов своей ценности? Или что устойчивые валюты, вроде немецкой марки и японской иены, варьировались бы между высокими и низкими курсами по отношению к доллару США до 40 процентов? Кто ожидал бы в прошлом году, что цены на нефть удвоятся? Или что ставка банковского процента будет устойчиво увеличиваться в течение прошлого года? Большинство крупных компаний материально зависят от одного или большего количества этих макроэкономических переменных. Для них, прокладывающих курс в среде изменчивых ставок банковского процента, курсов обмена валюты, и товарных цен, - это действительно опасный бизнес. В отличие от операционных рисков, в данном случае компания не контролирует изменение этих переменных. Но в то же время, хотя вы и не управляете ветром, вы можете регулировать свои паруса. Предмет этой статьи - методы для оценки и управления этими макроэкономическими рисками.

Моделирование риска с использованием генерации сценария

Для моделирования макроэкономических рисков наиболее часто используется метод генерации сценария. Как следует из названия, этот метод заключается в генерации сценария для возможных значений переменной, например цены на нефть, на период больше текущего например на 5 лет. Как и в случае предсказания пути урагана, сотни или тысячи сценариев генерируются с использованием компьютерного моделирования. Каждый представляет собой уникальный набор значений, которые переменная может принимать. Сценарии затем суммируются в распределение вероятности переменной. Важно иметь в виду, что это не предсказание изменения цены или курса. Генерация сценария – это скорее метод оценки величины и частоты возможного отклонения переменной от ожидаемого значения.

Прежде чем моделировать макроэкономическую переменную, необходимо понять ее фундаментальные характеристики. Ниже следуют некоторые типичные характеристики макроэкономических переменных.

1. Долгосрочный тренд. Для большинства переменных, отражающих исторические данные за большой период времени, в данном случае строится линия тренда, отражающая основные факторы, от которых зависит переменная. Например, долгосрочный тренд цен на нефть основан на таких фундаментальных факторах как мировая добыча, разведка новых месторождений и мировой спрос на нефть.
2. Отклонения от среднего значения. Хотя переменные и имеют долгосрочные тенденции, всегда есть отклонения от основного тренда, вызванные рыночными событиями, такими как сокращение ОПЕК добычи нефти, или объявление Федеральным резервным управлением об изменении своих резервов. В некоторых случаях отклонение от долгосрочного тренда становится постоянным и устанавливает новый тренд. В других, отклонение имеет краткосрочный характер, и значение переменной возвращается назад к долгосрочному тренду. Первый тип отклонений называется скачкообразным процессом, тогда как второй называется процессом отклонения от среднего. Например, индивидуальные акции иногда показывают скачки, тогда как ставка процента и большое количество товарных цен имеют тенденцию отклоняться от тренда.
3. Связи с другими переменными. Существует два вида связей с другими переменными: причинные и корреляционные. Причинные связи – это когда причинно-следственные отношения между переменными могут быть явно выявлены. Например, курсы обмена валюты непосредственно воздействуют на ставки банковского процента в соответствующих странах. Как растет в Соединенных Штатах ставка процента, так же и должен расти курс доллара США, а иначе это создаст арбитражные возможности. Есть формальные математические соотношения между курсами валют и процентными ставками, называемые паритетом процентной ставки. В других случаях, две переменные могут проявлять некоторую корреляцию, хотя явно выделить причинно-следственную связь будет невозможно. Например, цена на нефть и цена на природный газ движутся независимо, хотя между ними и есть некоторая корреляция. Отражение этих взаимосвязей жизненно важно для генерации сценария для всех переменных, включенных в него.
4. Сезонность. Большое количество предметов потребления имеют сезонные циклы в своем ценовом движении. Например, такие циклы имеет природный газ - между летними и зимними ценами, так как спрос изменяется в зависимости от времени года.
5. Хаотичность. Даже после суммирования вышеупомянутых характеристик, большинство переменных все еще имеют существенный уровень нестабильного поведения из-за "шума". Шум – это совокупный эффект множества небольших причинных факторов. Это отражается во многих непостоянных и независимых движениях, которые не являются значительными как в направлении, так и в размере.

Математический аппарат генерации сценария

Математический аппарат, наиболее часто используемый для отражения этих характеристик в разработке сценария, называется стохастическими дифференциальными уравнениями. Дифференциальные уравнения так названы, потому что они отражают различие между значением переменной во время t и значением на период позже (t+1). Таким образом, процесс разработки сценария начинается с текущего значения и, используя дифференциальное уравнение, затем высчитываются последовательно значения переменной в последующих периодах. Стохастическим дифференциальное уравнение называется потому, что содержит имеет случайный член, отражающий нашу неопределенность относительно ее движения на каждом последующем шаге.

Обычная форма дифференциального уравнения:

dV_t = f(V_mean – V_t) + g(V_t, W_t, X_t, Y_t) * dt + h(V_t) * dZ

Давайте кратко рассмотрим каждый член этого уравнения, чтобы связать их с характеристиками, которые мы пытаемся моделировать.  

• Первый член, dV_t, это изменение значения переменной, V, со времени t до t+1, то есть, V_t+1 – V_t. Это именно то, что мы и ищем.
• f(V_mean – V_t) – функция возвращения к среднему. Она отражает степень, с которой переменная имеет тенденцию возвращаться назад к своему фундаментальному долгосрочному уровню всякий раз, когда отклоняется от него. Всякий раз, когда текущая значение V_t, становится выше своего среднего уровня V_mean, эта функция принимает отрицательные значения, и наоборот. Для переменных, показывающих "скачки", этот член заменяется функцией, которая моделирует нечастые большие скачки к новому уровню.
• g(V_t, W_t, X_t, Y_t) - функция, которая показывает, как движение переменной V связано с другими потенциальными переменными W, X, и Y. Эта функция используется, чтобы воспроизвести причинные соотношения, линию тренда, краткосрочные отклонения и сезонность. Часто этот член разбивается на несколько функций, каждая из которых отражает одну из этих характеристик.
• h(V_t) * dZ - член, который отражает случайное движение или шум. Тогда как другие составляющие уравнения детерминированы. dZ - значение стандартной нормальной случайной переменной. Ее распределение вероятности имеет привычную форму колокола, сосредоточенную в ноле со стандартным отклонением 1. Когда дифференциальное уравнение используется итеративным способом, на каждом следующем шаге, dZ случайным образом принимает значение согласно своего закона распределения вероятности. h(V_t) - фактор вычисления случайного движения. Это член дифференциального уравнения, который имеет различные значения, каждый раз когда мы генерируем новый сценарий. Он также используется, чтобы отразить корреляцию с другими переменными.

Каждый элемент справа от знака равенства это математическая функция, чья структура и параметры должны быть определены специально для переменной, которую они отражают. Например, функция возвращения к среднему для сырой нефти может выглядеть как: -1.10 * (V_mean - V_t) * dt. Коэффициент возвращения (в этом случае он равен 1.1) показывает скорость, с которой краткосрочное отклонение, как ожидается, исчезнет. "Половина жизни" отклонения – время, за которое отклонение уйдет от фундаментального уровня, как ожидается, наполовину - равно ln (2) / коэффициент возвращения. В нашем примере, это будет 0.63 года или приблизительно 7.5 месяцев. Как только отклонение уменьшено на половину, требуется 7.5 других месяцев для того, чтобы его снова уменьшить на половину (1/4 первоначального отклонения). Это означает, что скорость, с которой значение изменяется в меньшую сторону по мере приближения к фундаментальному уровню. Обратите также внимание, что скорость среднего возвращения не зависит от значения Vmean, фундаментального уровня.

Определение функций и значений параметров уравнений требует строгого статистического анализа исторических данных. С помощью математического анализа было проверено насколько хорошо стохастические дифференциальные уравнения отражают фундаментальные характеристики, которые упоминались выше.

Давайте взглянем на некоторые результаты использования этих уравнений при генерации сценариев поведения сырой нефти и природного газа (рисунки 1 и 2). Они основаны на наборе уравнений, разработанных доктором Едуардо Шварцом (UCLA) и доктором Джимом Смитом (Герцогской Университетская Школа Бизнеса Fuqua) и названных в их честь двухфакторной моделью товарных цен. «Двухфакторная» потому, что модель учитывает и долгосрочную тенденцию цен и возвращение к среднему от краткосрочных скачков, как расширение традиционных моделей, рассматривающих только долгосрочные тенденции. Модель отражает все характеристики, которые мы обсудили выше, среднее возвращение, корреляция двух товаров, сезонность, и хаотичность.

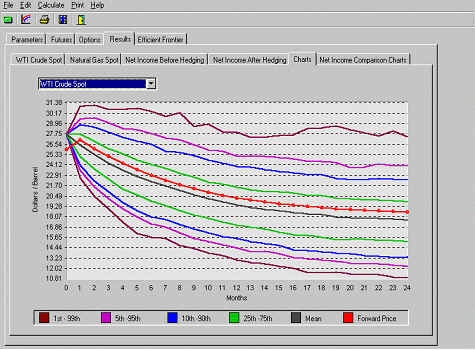
Рис. 1. Распределение WTI цен на нефть

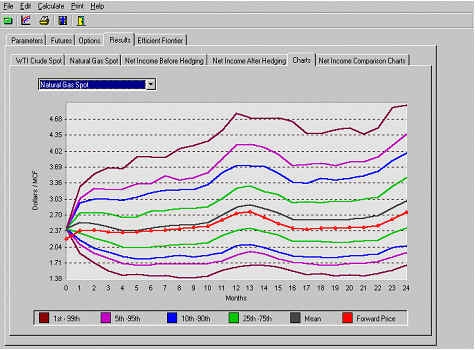
Рис. 2. Распределение цен на природный газ

Рисунки 1 и 2 иллюстрируют суммарную статистику генерации 1000 сценариев динамики сырой нефти и природного газа, соответственно, на протяжении 24 месяцев (с ноября 1999 года). Черная кривая показывает, для каждого месяца, среднее значение цены среди всех 1000 сценариев. Остальные цветные линии показывают различные составляющие цены в каждом месяце. Хотя только некоторые составляющие показаны, но так как мы имеем все данные от 1000 моделирований сценария, мы можем отразить полной распределение вероятности цены на каждый месяц.

Отношение рисков к финансовым показателям

Моделирование макроэкономических переменных само по себе не стоит многого, если мы не можем перевести это в воздействие на общую финансовую метрику, такие показатели как наличный поток или чистый доход. Это все равно что измерять направление и скорость ветра, но не смотреть как это влияет на ваш курс. Жизненно важно анализировать суммарное воздействие всех переменных риска на финансовые показатели, чтобы получить портфельные выгоды диверсификации риска. Простой метод связи финансовых показателей с макроэкономическими переменными это использование статистических методов таких как мультипликативная регрессия. Независимые переменные - переменные риска, типа товарных цен, и зависимая переменная - финансовый показатель, типа чистого дохода. Более продвинутые методы, такие как обобщенные линейные модели или нейронные сети могут также применяться, для исследования связи между источниками риска и финансовыми показателями. Четкое соединение финансового показателя и источников риска позволяет нам развивать сценарии и распределения вероятности для финансового показателя точно также, как мы это делали для переменных риска.

Хеджирование рисков

Теперь, когда мы количественно определили риски и их влияние, заключительным шагом должно быть определение того, как смягчить риск. Наиболее обычный метод для смягчения воздействия макроэкономических рисков состоит в том, чтобы хеджировать (застраховать) их на финансовых рынках. Финансовые рынки для хеджирования процентных ставок, курсов валют, товарных цен хорошо развиты и предлагают значительную ликвидность, что позволяет минимизировать транзакционные издержки. Генерируя сценарии для каждой переменной риска, нужно анализировать альтернативу хеджирования рисков напрямую.

Например, давайте предположим, что мы рассматриваем нулевой воротник выбора стоимости на WTI сырье в течение следующих 12 месяцев. Нулевой воротник выбора стоимости включает покупку помещенного выбора и продажи запрошенного выбора страхового взноса так, чтобы чистая транзакционная стоимость была нулевая. Следующие две диаграммы показывают неуверенность в чистом доходе до и после осуществления стратегии хеджирования.

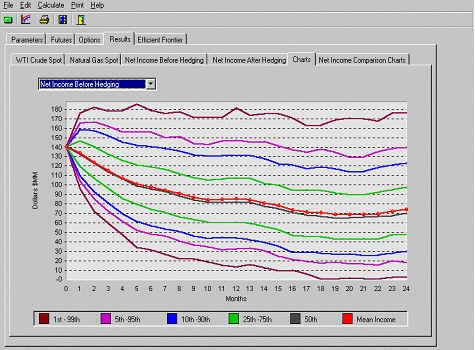
  Рис. 3. Распределение чистого дохода до хеджирования

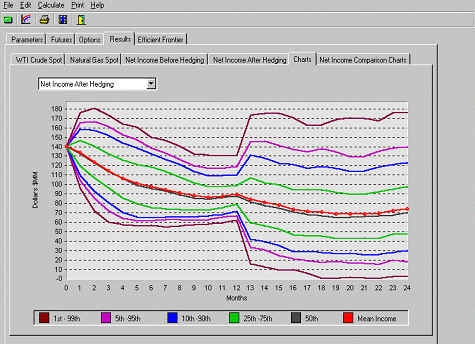
Рис. 4. Распределение чистого дохода после хеджирования

Обратите внимание, что хедж эффективно размещает ограничение на чистый доход, но забирает некоторый потенциал сверху. Отказ от некоторого потенциального дохода стоит того, чтобы защититься от неблагоприятного исхода? Конечно, моделирование не может ответить на этот вопрос. На ответ здесь влияют предпочтения риска/выигрыша команды управления. Однако, моделирование макроэкономических рисков обеспечивает неоценимой информацией, которая помогает компаниям ориентироваться среди этих вариантов, чтобы принимать решения согласно своим целям..

Генерация сценариев с использованием стохастических дифференциальных уравнений - строгая техника моделирования, которая требует навыка и опыта. Менеджеры должны брать ответственность за:

• Обеспечение, чтобы уравнения должным образом отражали фундаментальные характеристики источников риска и соответствия произведенным сценариям
• Использование аналитиков, которые являются квалифицированными специалистами в статистике, теории вероятности, и компьютерном моделировании
• Развитие и анализ финансовых стратегий хеджирования в соответствии с своими предпочтениями соотношения риска/выгоды

Без надлежащего моделирования и управления макроэкономических рисков, компания полностью покоряется ветру.