Прежде всего заметим, что было бы ошибкой принять связь между стимулом и ответной реакцией за систему обратной связи. Этот термин стал настолько вольно использоваться в ряде мест, что почти всякая реакция на любое действие принимается за обратную связь.

Содержание этого термина следует вскрыть с известной осторожностью, поскольку он относится к фундаментальным понятиям кибернетики. Для его объяснения нам придется привести небольшое математическое описание в самой общей форме в надежде на то, что это поможет правильно понять термин даже читателям, далеким от математики.

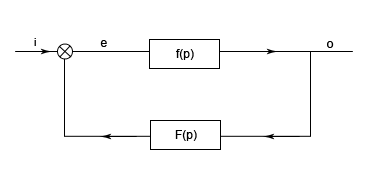
На вход системы обратной связи подается выходная величина самой системы - o. Выходная величина системы обратной связи есть результат воздействия на величину o функции преобразования системы обратной связи, т.е. oF(p). На входе предыдущей системы в результате воздействия обратной связи вместо величины i будет величина e = i + oF(p).

Если это так, то форма функции преобразования первичной системы изменится. Первоначально мы ее записали как f(p) = o / i, но теперь это неверно. На входе основной системы (прямоугольник f(p)) теперь уже величина не i, а e, представляющая суммарный эффект входной величины i и величины, обусловленной действием обратной связи, oF(p).

Поскольку на входе блока f(p) величина e, а на выходе o, то f(p) = o / e. Чтобы получить функцию преобразования всей системы, мы должны вернуться к основному определению, в котором выходная величина сравнивалась с входной, и записать новую функцию ?(p), которая устанавливает правильное соотношение между функциями f(p) и F(p). Конечно, просто записать ?(p) = o / i. Но чтобы сделать то, что нам нужно, перепишем уравнение для первой системы f(p) и уравнение для e. Тогда получим

?(p) = o / i = f(p) / [1 - f(p)F(p)].

Из данного уравнения следует несколько выводов. Во-первых, видно, что обратная связь может стать либо положительной, либо отрицательной.

Рассмотрим поизведение функций первичной цепи и цепи обтратной связи, а именно f(p)F(p). Предположим, что система не требует коррекции, т.е. функция обратной связи не оказывает никакого влияния. Тогда перемножение функций даст нуль и общая функция преобразования ?(p) будет правильно работать как f(p) сама по себе. Если произведение функций будет больше нуля, то знаменатель станет меньше единицы, а общее значение функции больше значения функции преобразования первичной цепи - в итоге получится положительная обратная связь. Если произведение функций станет меньше нуля, то знаменатель станет больше единицы и значение результирующей функции станет меньше значения функции преобразования первичной цепи - получим отрицательную обратную связь. Очевидно, что в одной и той же системе может быть как положительная обратная связь, так и отрицательная, в зависимости от формы переменной, действующей на входе, и сдвига по фазе во взаимодействии этих двух цепей.

Во-вторых, весьма интересен результат действия отрицательной обратной связи. Корректирующая обратная связь по необходимости должна быть отрицательной, если любое отклонение от заданной нормы считается по его абсолютному значению положительным. Тогда уравнение для e должно быть переписано как e = i - oF(p), поскольку нам известно, что абсолютное значение функции преобразования погрешности должно вычитаться из первичного значения входной величины. Тогда уравнение для общей функции преобразования следует переписать в виде

?(p) = f(p) / [1 + f(p)F(p)].

Анализируя это уравнение, можно определить, что происходит, если значение функции преобразования первичной цепи становится очень большой величиной. При значении f(p), существенно превышающем единицу, единицей в знаменателе можно пренебречь и сократить числитель и знаменатель на f(p). В таком случае в схеме с обратной связью определяющей станет функция преобразования цепи обратной связи. Формально это можно записать так:

если |f(p)| >> 1, то ?(p) ? 1 / F(p).

Результат поразителен. У нас может быть очень слабый сигнал на входе, как это часто случается в биологических и управляющих ситуациях. Мы можем сильно усиливать этот сигнал в первичной цепи, и это часто случается. Тогда можно предположить, что любой "шум" на входе, т.е. по смыслу любая неверная информация на входе, станет также сильно усиливаться. Но поскольку в системе в целом преобладает влияние не первичной цепи, не первичной системы, а системы обратной связи, то именно она обеспечит на выходе сигнал, значительно "чище", чем можно было ожидать. Неважно, какого сорта шум действует на систему, как он велик по сравнению с входным сигналом, насколько он хаотичен и почему возник. Система стремится подавить его влияние.